Geo. Practical Data Analysis : Measurement of Dispersion
12th Geography Practical Part 3 Analysis: Measurement of Dispersion
इ. बारावी भूगोल प्रात्यक्षिक क्र 3 विदा विश्लेषण: अपस्करणाचे मापन
Geo Practical Data Analysis Measurement of Dispersion
माहीतीचे विश्लेषण–
चलानुसार माहीतीची मांडणी केल्यावर तिचे विश्लेषण केले जाते किंवा निष्कर्ष काढले जातात. त्यासाठी विविध पध्दती वापरता येतात.
1) चल व माहिती यांच सहंसबंध जाणून घेवून.
2) पाहून व टक्केवारीची तुलना करुन किंवा मध्य काढून
3) सहसंबंध काढून अंदाज व्यक्त करुन
दिलेल्या सामग्रीत मध्यवर्ती मूल्यापांसून एखादे मुल्यकिती दुर आहे किंवा विखुरलेले आहे हे जाणून घेणे यालाच अपस्करण म्हणतात ते दोन प्रकारे शोधता येते. 1) दिलेल्या माहीतीची कक्षा माहीत करुन व 2) दिलेल्या माहीतीचे प्रमाण विचलन जाणून घेऊन.
प्रात्यक्षिकाचा उद्देश– दिलेल्या साख्यिकीय माहीतीचे मांडणी करुन तिचे विश्लेषण करणे.
उद्दिष्टे-
1) दिलेल्या साख्यिकीय माहीतीची कक्षा शोधणे.
2) दिलेली साख्यिकीय माहिती मध्याच्या भोवती केद्रीत आहे किंवा विखुरलेली आहे त्याचे विश्लेषण करणे.
3) दिलेल्या साख्यिकीय माहीतीचे प्रमाण विचलण व भिन्नतेचा गुणांक शोधून त्यातील सहसंबध / विचलनाचे प्रमाण शोधणे.
इ. बारावी भूगोल प्रात्यक्षिक क्र 3 विदा विश्लेषण: अपस्करणाचे मापन
Geo Practical Data Analysis Measurement of Dispersion
उदा.1 खालील साख्यिंकीय माहीतीच्या अनुशंगाने मध्य काढून प्रमाण विचलन व भिन्नतेचे गुणक काढा
| नगर | शहराच्या मध्य भागापासून झालर क्षेत्राचे अंतर किमी मध्ये |
| A | 4 |
| B | 9 |
| C | 11 |
| D | 12 |
| E | 15 |
| F | 5 |
| G | 8 |
| H | 12 |
| I | 14 |
A) मध्य (X)
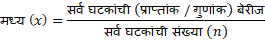
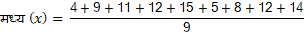
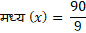
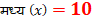
B) कक्षा
सांख्यिकीय माहीतीची कक्षा = सामग्रीतील कमाल मूल्य – सामग्रीतील किमान मूल्य
= 15 – 4
= 11
सांख्यिकीय माहीतीची कक्षा = 11
c) प्रमाण विचलन-
| नगर | शहराच्या मध्य भागापासून झालर क्षेत्राचे अंतर किमी मध्ये | (X1-X) | (X1-X)2 | |
| A | 4 | -10 = | -6 | 36 |
| B | 9 | -10= | -1 | 1 |
| C | 11 | -10= | 1 | 1 |
| D | 12 | -10= | 2 | 4 |
| E | 15 | -10= | 5 | 25 |
| F | 5 | -10= | -5 | 25 |
| G | 8 | -10= | -2 | 4 |
| H | 12 | -10= | 2 | 4 |
| I | 14 | -10= | 4 | 16 |
| ∑ (X1-X)2 = | 116 | |||
| ∑ (X1-X)2 = 116 |
प्रमाण विचलन (sd) = 3.59
विचलनाचे मुल्य हे आलेल्या मध्यमुल्य (10) पेक्षा निम्म्याहून कमी आहे. त्यामुळे आलेले विचलन हे विखूरलेल्या
स्वरुपात आहे असे म्हणता येईल.
D) भिन्नतेचे गुणक (CV) –
भिन्नतेचे गुणक (cv) = 35.9
वरील साख्यिंकीय माहीतीचे भिन्नतेचे गुणांक, प्रमाण विचलनाचे मध्य आणि विदेच्या मूल्यामध्ये 35.9 % विचलन दर्शवीत आहे.
Geo. Practical Data Analysis : Measurement of Dispersion
Geo Practical Data Analysis Measurement of Dispersion
उदा. क्र 02
| नगर | अंक |
| A | 9 |
| B | 2 |
| C | 5 |
| D | 4 |
| E | 12 |
| F | 7 |
| G | 8 |
| H | 11 |
| I | 9 |
| J | 3 |
| K | 7 |
| L | 4 |
| M | 12 |
| N | 5 |
| O | 4 |
| P | 10 |
| Q | 9 |
| R | 6 |
| S | 9 |
| T | 4 |
A) मध्य (X)
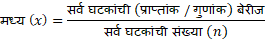
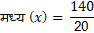
मध्य (X) = 7
————————————–
B) कक्षा
सांख्यिकीय माहीतीची कक्षा = कमाल मूल्य – किमान मूल्य
= 12 – 2
= 10
सांख्यिकीय माहीतीची कक्षा = 10
————————————–
C) प्रमाण विचलन-
| नगर | अंक | (X1-X) | (X1-X)2 |
| A | 9-7 | 2 | 4 |
| B | 2-7 | -5 | 25 |
| C | 5-7 | -2 | 4 |
| D | 4-7 | -3 | 9 |
| E | 12-7 | 5 | 25 |
| F | 7-7 | 0 | 0 |
| G | 8-7 | 1 | 1 |
| H | 11-7 | 4 | 16 |
| I | 9-7 | 2 | 4 |
| J | 3-7 | -4 | 16 |
| K | 7-7 | 0 | 0 |
| L | 4-7 | -3 | 9 |
| M | 12-7 | 5 | 25 |
| N | 5-7 | -2 | 4 |
| O | 4-7 | -3 | 9 |
| P | 10-7 | 3 | 9 |
| Q | 9-7 | 2 | 4 |
| R | 6-7 | -1 | 1 |
| S | 9-7 | 2 | 4 |
| T | 4-7 | -3 | 9 |
| ∑ (X1-X)2 = | 178 | ||
∑ (X1-X)2 = 178
* निष्कर्ष– विचलनाचे मुल्य हे आलेल्या मध्यमुल्य (7) पेक्षा निम्म्याहून कमी आहे. त्यामुळे आलेले विचलन हे विखूरलेल्या स्वरुपात आहे असे म्हणता येईल.
—————————
D) भिन्नतेचे गुणक-
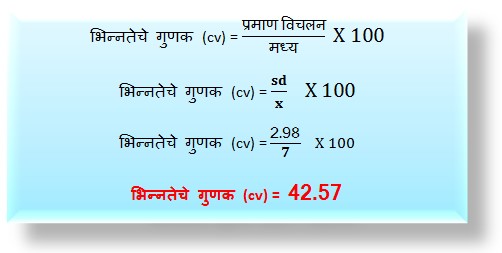
वरील साख्यिंकीय माहीतीचे भिन्नतेचे गुणांक, प्रमाण विचलनाचे मध्य आणि विदेच्या मूल्यामध्ये 42.57% विचलन दर्शवीत आहे
Geo Practical Data Analysis Measurement of Dispersion
उदा. क्र .3
दिलेली आकडेवारी वेगवेगळया नगरांमध्ये निवासी भूमी उपयोजनाखालील टक्केवारी दर्शवीते तिचा मध्य व कक्षा काढून प्रमाण विचलन व भिन्नतेचे गूणक काढा.
| नगर | अंक |
| A | 57 |
| B | 64 |
| C | 63 |
| D | 67 |
| E | 49 |
| F | 59 |
| G | 44 |
| H | 47 |
| I | 61 |
| J | 59 |
A) कक्षा-
माहितीची कक्षा = कमाल मुल्य – किमान मुल्य
माहितीची कक्षा = 67 – 44
माहितीची कक्षा = 23
—————————————
B) मध्य–
—————————————
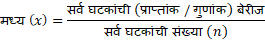
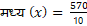
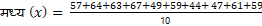
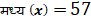
C) प्रमाण विचलन-
| नगर | अंक | ( X1-X ) | (X1 – X)2 |
| A | 57 | 57 – 57 = 0 | 0 |
| B | 64 | 64 – 57 = 7 | 49 |
| C | 63 | 63 – 57 = 6 | 36 |
| D | 67 | 67 – 57 = 10 | 100 |
| E | 49 | 49 – 57 = -8 | 64 |
| F | 59 | 59 – 57 = 2 | 4 |
| G | 44 | 44 – 57 = -13 | 169 |
| H | 47 | 47 – 57 = -10 | 100 |
| I | 61 | 61 – 57 = 4 | 16 |
| J | 59 | 59 – 57 = 2 | 4 |
| ∑ (X1-X)2 = | 542 |
∑ (X1-X)2 = 542
प्रमाण विचलन (sd) = 7.36
प्रमाण विचलनाचे मूल्य हे मध्य मूल्याच्या (23) अर्ध्यापेक्षा ही कमी आहे. म्हणजेच विचलन नगरांमध्ये निवासी भूमी उपयोजनाखालील क्षेत्र विखुरलेले दाखवते.
—————————————-
4) भिन्नतेचे गुणक–
भिन्नतेचे गुणक (cv) = 12.91
निष्कर्ष- वरील साख्यिंकीय माहीतीचे भिन्नतेचे गुणांक, प्रमाण विचलनाचे मध्य आणि विदेच्या मूल्यामध्ये 12.91% विचलन दर्शवीत आहे.
उदा क्र 4
प्रमाण विचलनाची गणना करा. आलेल्या उत्तराचे विश्लेषण करा.
| गाव | लोकसंख्या |
| A | 500 |
| B | 200 |
| C | 300 |
| D | 400 |
| E | 250 |
| F | 350 |
| G | 450 |
A ) कक्षा
माहितीची कक्षा = कमाल मुल्य – किमान मुल्य
माहितीची कक्षा = 500 – 200
माहितीची कक्षा = 300
———————————————
B) मध्य
—————————–
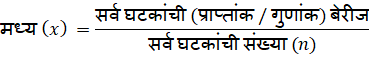
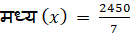
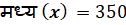
C ) प्रमाण विचलन-
| गाव | लोकसंख्या | (X1-X) | (X1-X)2 | |
| A | 500 | 500 – 350 | 150.00 | 22500 |
| B | 200 | 200 – 350 | -150.00 | 22500 |
| C | 300 | 300 – 350 | -50.00 | 2500 |
| D | 400 | 400 – 350 | 50.00 | 2500 |
| E | 250 | 250 – 350 | -100.00 | 10000 |
| F | 350 | 350 – 350 | 0.00 | 0 |
| G | 450 | 450 – 350 | 100.00 | 10000 |
| ∑ (X1-X)2 = | 70000 | |||
∑ (X1-X)2 = 70000
निष्कर्ष-
प्रमाण विचलनाचे मूल्य हे मध्य मूल्याच्या (350) अर्ध्यापेक्षा ही कमी आहे. म्हणजेच दिलेल्या माहितीचे विचलन विखुरलेल्या स्वरुपात आहे.
———————————-
D) भिन्नतेचे गुणक
निष्कर्ष-
वरील साख्यिंकीय माहीतीचे भिन्नतेचे गुणांक, प्रमाण विचलनाचे मध्य आणि विदेच्या मूल्यामध्ये 28.57 % विचलन दर्शवीत आहे
उदा. 5 .
खालील विदा शिमला येथील 10 वर्षातील पहिल्या हिमवृष्टीचा दिवस (उदा., 291 वा दिवस) दर्शविते. या दिवसांच्या कक्षेची गणना करा. तसेच मध्य व प्रमाण विचलनाची गणना करा व आलेल्या उत्तराचे विश्लेषण करा.
| नगर | शहराच्या मध्य भागापासून झालर क्षेत्राचे अंतर किमी मध्ये |
| A | 291 |
| B | 299 |
| C | 279 |
| D | 302 |
| E | 280 |
| F | 303 |
| G | 299 |
| H | 304 |
| I | 307 |
| J | 316 |
A ) कक्षा
माहितीची कक्षा = कमाल मुल्य – किमान मुल्य
माहितीची कक्षा = 316 – 279
माहितीची कक्षा = 37
———————————-
B) मध्य–
———————————
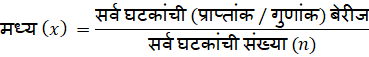
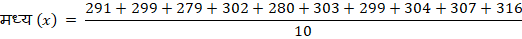
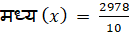
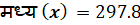
C ) प्रमाण विचलन-
| नगर | शहराच्या मध्य भागापासून झालर क्षेत्राचे अंतर किमी मध्ये | (X1-X) | (X1-X)2 | |
| A | 291 | 291-297.80= | -6.8 | 46.24 |
| B | 299 | 299-297.80= | 1.2 | 1.44 |
| C | 279 | 279-297.80= | -18.8 | 353.44 |
| D | 302 | 302-297.80= | 4.2 | 17.64 |
| E | 280 | 280-297.80= | -17.8 | 316.84 |
| F | 303 | 303-297.80= | 5.2 | 27.04 |
| G | 299 | 299-297.80= | 1.2 | 1.44 |
| H | 304 | 304-297.80= | 6.2 | 38.44 |
| I | 307 | 307-297.80= | 9.2 | 84.64 |
| J | 314 | 314-297.80= | 16.2 | 262.44 |
| ∑ (X1-X)2 = | 1149.6 | |||
∑ (X1-X)2 = 1149.6
प्रमाण विचलन (sd) = 10.72
निष्कर्ष-प्रमाण विचलनाचे मूल्य हे मध्य मूल्याच्या अर्ध्यापेक्षा ही कमी आहे. म्हणजेच दिलेल्या माहितीचे विचलन विखुरलेल्या स्वरुपात आहे.
D) भिन्नतेचे गुणक–
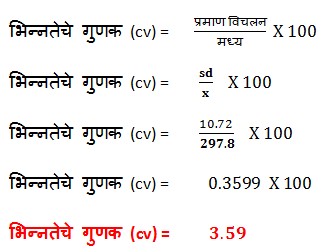
निष्कर्ष-
वरील साख्यिंकीय माहीतीचे भिन्नतेचे गुणांक, प्रमाण विचलनाचे मध्य आणि विदेच्या मूल्यामध्ये 3.59 % विचलन दर्शवीत आहे
बारावी भूगोल प्रात्यक्षिक 1 सर्वेक्षण (सोडविलेले )
बारावी भूगोल प्रात्यक्षिक क्र. 2 विदा विश्लेषण-
बारावी भूगोल प्रात्यक्षिक 1 सर्वेक्षण (सोडविलेले )
[…] Geo Practical Data Analysis Measurement of Dispersion […]
[…] Geo Practical Data Analysis Measurement of Dispersion […]
[…] Geo Practical Data Analysis Measurement of Dispersion […]